Die Vorlesung Kognitive Systeme am KIT 2012/2013 zusammengefasst von honnel und famalgosner

Kognitive Systeme

Allgemeine Infos

k-Means Algorithmus aka Clustering
Phase und Spektrum sind notwendig um ein Bild vollständig zu rekonstruieren

Themen in den Klausuren

Signalverarbeitung

Fouriertransformation

Die muss man drauf haben: 🙁

Fouriertransformationen

Abtasttheorem
Windowing
Overlap Processing
Zeichnen von Spektrum
x-Achse: Frequenz, y-Achse: Real-Teil, z-Achse: Imaginär-Teil
Überführen von f(t) mit Hilfe trigonometrischen Additionsthreorems in eine Form mit n Termen
Bild alle f Hz wiederholen
Höhe mit f = 1/T multiplizieren (T = 2 in Tabelle oben)
Zeichnen von Betragsspektrum
x-Achse: Frequenz, y-Achse: sqrt(R(F(w))²+I(F(w))²)

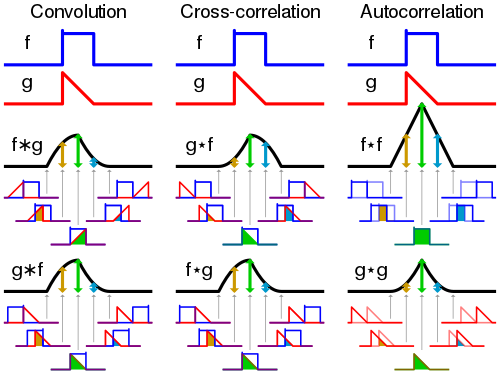
Faltung

Sehr gutes Applet zum Falten

Autokorrelation

Komplexe Faltung

Gegeben: f(x), g(x)
Gesucht: f(x)*g(x)
Ablauf

Spiegeln von f(x)
Durchschieben von f(x)
Aufsummieren der geschnittenen Flächen

max(f(x)*g(x)) = max. Amplitute(f(x)) * max. Amplitute(g(x)) * Länge(f(x)), Die Länge bezieht sich auch den jeweiligen Peak der gerade durchgeschoben wird
Sonderfall Faltung mit Dirac-Funktion:
Kopiert andere Funktion und skaliert sie entsprechend Faktor A in A·δ(x - x_0)
(A = späteres Maximum)
Keine Spiegelung falls f(x) = Dirac

Filter

Tiefpassfilter

Verwendung: Glättung, Rauschelimination

Mittelwertfilter
1, 1, 1
1/9 * ( 1, 1, 1 )
1, 1, 1
Gauß-Filter
Definiert durch zweidimensionale Gauß-Funktion (dies approximiert durch 3×3-Filter)

1, 2, 1
1/16 * ( 2, 4, 2 )
1, 2, 1

Hochpassfilter

Verwendung: Kantendetektion

Prewitt
X-Filter: gute vertikale, schlechte horizontale Kantendetektion

-1, 0, 1
-1, 0, 1
-1, 0, 1

Y-Filter: schlechte vertikale, gute horizontale Kantendetektion

-1, -1, -1
0, 0, 0
1, 1, 1

Operator: Kombination aus X- und Y-Filter -> Bestimmung des Grauwertgradientenbetrages
Sobel
X-Filter: gute vertikale, schlechte horizontale Kantendetektion

-1, 0, 1
-2, 0, 2
-1, 0, 1

Y-Filter: schlechte vertikale, gute horizontale Kantendetektion

-1,-2,-1
0, 0, 0
1, 2, 1

Operator: Kombination aus X- und Y-Filter -> Bestimmung des Grauwertgradientenbetrages
Laplace
gute Kantendetektion

0, 1, 0
1,-4, 1
0, 1, 0

Aber: sehr anfällig für Bildrauschen, daher vorher oft noch Gauß-Filter zur Glättung (Laplacian of Gaussian)
Roberts
gute diagonale Kantendetektion
Filtermasken
R_x: (-1,0,0,1)
R_y: (0,-1,1,0)
Filterfunktion: |R_x*b[x,y]| + |R_y*b[x,y]|

Unterschied zwischen Prewitt, Sobel und Laplace:

Prewitt und Sobel erkennen die Steigung der Funktion (erste Ableitung)
Laplace erkennt die Änderungsrate (zweite Ableitung) -> Detektion sowohl in horizontaler, vertikaler und diagonaler Richtung

Canny-Kantendetektor

Optimale Kantenerkennung, 0 = keine Kante, 255 = Kante

Gauß-Filter
Prewitt_X und Prewitt_Y oder Sobel_X und Sobel_Y
Non-Maximum Supression: Gradient muss lokales Maximum sein bei Betrachtung der zwei direkten Nachbarn entlang der Gradientenrichtung
Hysterese-Schwellwertverfahren

* Verwendung von 2 Schwellen: low/high
* Pixel wird akzeptiert wenn Gradient über Schwellwert high
* 8 Nachbarn müssen mit Gradient über Schwellwert low liegen

Kombinierte Operatoren

Laplacian of Gaussian

Schwellwertfilter

Img'(u,v) = q falls Img(u,v) <= T(reshhold)
0 sonst

Maschinelles Lernen

parametrisches Lernen
setzt Wahrscheinlichkeitsdichtefunktion voraus, deren Parameter an Hand der Trainingsdaten geschätzt werden (Gauss-Klassifikator)
nicht-parametrisches Lernen
setzt keine explizite Funktion voraus, lernt Wahrscheinlichkeiten aus Trainingsdaten (Parzen Fenster, k-nearest-neighbour, Perzeptron,…)

Klassifikation

Bayes Entscheidungstheorie

Wissen und Bestandteile erklären können

2-Klassen Problem

Gegeben:

P(A), P(B), P(x|A), P(x|B); Dabei gilt: P(A)+P(B) = 1

a) Man hat Gauß-Verteilungen gegeben für P(x|A), P(x|B)

b) Man hat Plots der Verteilungen gegeben

Vorgehensweise für a):

P_error Formel aufstellen (Integrale), Vorfaktoren rausziehen
Optimalen Schwellwert bestimmen: Gleichsetzen von beiden Fehlerwahrscheinlichkeiten
Ergebnis von 2 in Formel von 1 einsetzen und Grenzen der Integrale anpassen, sowie auf passenden Form für Sigma-Tabelle bringen (Interal von -∞ bis opt Grenze)

Vorgehensweise für b):

P(A) = x * P(B) und P(A) + P(B) = 1 -> P(A) und P(B) bestimmen
Optimalen Schwellwert graphisch bestimmen: P(A) * P(x|A) und P(B) P(x|B) zeichen (x-Werte bleiben gleich, y-Werte anpassen)
P_error = Überlappungsfläche der beiden Fehlerwahrscheinlichkeiten

Neuronale Netze

Overfitting: Überanpassung des Modells an den Datensatz. Es fehlt dann an Generalisierung und Schließen auf Neues funktioniert dann schlecht (Lösung: Anzahl der Interationen beim Trainieren gering halten).
Generalisierbarkeit: Fähigkeit auch nicht im Training enthaltene Daten richtig zu klassizifieren
Aufgabentyp: Netz malen aus Graph
(Aufpassen bei manchen Klausuren Aktivierungsfunktion definiter mit <, > dann ist = undefiniert; in andernen Klausuren ist <= und >)

Lineare Funktionen ablesen und in Ungleichungen der Form ax+by>=Theta bringen (Theta= y Achsenabschnitt, a und b sind Steigungen
a und b sind die Gewichte an den Kanten, Theta ist der Schwellwert eines Perzeptrons
Für nächst höhere Stufe die Ungleichungen mit einander Addieren und 2. wiederholen

Aufgabentyp: Netz malen aus binärer Funktion
Hier einfach Primitive zusammenstöpseln

Wissensrepräsentation

Planung

Homogene projektive Geometrie

Gesamtprojektionsmatrix P = (K*R|K*t)

Quaternionen

Roationsmatrix in Quaternion
SLERP
Berechnet für t in [0,1] die kürzeste Verbindung auf der 4D-Einheitsphäre zwischen zwei Quaternionen q und r
Analytisch: SLERP(q,r,t) = q*(rq^-1)^t

Bildverarbeitung

Lokale Punktmerkmale = Texturmerkmale

Punktoperatoren

homogene:
Img'(u,v) = f(Img(u,v))
unabhängig von der Position bzw. den Nachbarpixeln
Implementierung oft als Look-Up-Table
affine:
f:[0..q] -> [0..q], x -> ax+b
a, b legen Funktion fest
Anwendung:
Kontrasterhöhung: b=0, a>1
-verminderung: b=0, a0, a=1
-verminderung: b<0, a=1 * Invertierung: b=q, a=-1 (q = max. Wert) * Kombinationen:b=-50, a=2 * nicht-affine: * beliebige Abbildungsfunktion f:[0..q] -> [0..q]
Anwendung: Ausgleich von Sensor-Nichtlinearität, Gewichtung, Binarisierung
morphologische:
Erosion: Auswahl verkleinern
Dilatation: Auswahl vergrößern
Öffnen-Operation: Erosion -> Dilatation
Schließen-Operation: Dilatation -> Erosion

Automatische Kontrastanpassung

Grauwerthistogramm

Häufigkeit eines Grauwerts im Bild
H(x) = #(u,v):I(u,v) = x, x in [0..q-1]

Spreizung

Berechnet min/max-Werte und bildet diese linear auf [0..255] ab.
Nur sinnvoll wenn 0 und 255 noch nicht vorkommen! (nicht robust)
Kann als eine affine Punktoperation ausgedrückt werden
Abbildungsvorschrift:

I(u,v) – min
I'(u,v) = q * _____________
max – min

Histrogrammausdehnung

Verbesserung der Spreizung
Statt min/max Intensität, Quantile und tatsächliche Maxima erkennen
Affine Punktopertion
Erfahrungsgemäß gute Werte sind das 0.1-Quantil und das 0.9-Quantil.
Vorgehensweise:

Histogramm bestimmen
Akkumuliertes Histogramm bestimmen

* Quantile Berechnen
* Histogrammdehnung bestimmen (Affine Punktoperation: I = aX+b)

Histogrammausgleich

Gleichverteilung im gesamten zur Verfügung stehenden Wertebereich
Häufige Grauwerte werden auseinandergezogen, weniger häufige zusammengeschoben
Vorgehensweise:

Histogramm bestimmen
Akkumuliertes Histogramm bestimmen

* H_n(x) = |q* H_a(x)/H_a(q)|, H_n = H_normiert, H_a = H_akkumuliert
* Kann zu einer Kontrastminderung führen:
* (0,255) -> (0,127)

Segmenierung: Punktmerkmal

Sum of squared Differences (SSD)

Wird minimal (=0) bei guter Übereinstimmung

Zero Mean Normalized Cross-Correlation (ZNCC)

Wird maximal (=1)bei guter Übereinstimmung

Iterative Endpoint Fit

Hough-Transformation

Ziel: Erkennung gerader Linien im Bild
Ansatz Stelle Linie durch Normalenvektor in Polarkoordination dar
Kurven für kollineare Punkte schneiden sich in genau 2 Punkten
r = x cos(phi) + y sin(phi)

Stereokameras

Epipolzeugs

Transformation

Sprachverarbeitung

Spracherzeugung

Anregung
Lunge: Erzeugung von Luftstrom
Larynx: Schwingung, Modulation eines periodischen Luftstroms
Vokaltrakt: Artikulation, Klangcharakter eines Phonems
Bei konstanter Vokaltraktkonfiguration kann durch Änderung der Anregungsfrequenz (Larynx) unterschiedliche Tonhöhen erzeugen

Vokale

Frequenzpeaks in Transferfunktion

i : 300, 2300Hz
a: 750, 1200Hz
u: 350, 800Hz

Allgemeines

Phonem
Ein Phonem ist ein Laut der für eine Sprache notwendig ist. Im Deutschen gäbe es also z.B. langes und kurzes a, stimmhaftes s etc. Z.B. stehen in einem Englischwörterbuch immer die Phoneme dabei (/th e/ etc.).
Formanten
Jedes Phonem hat charakteristische Grundfrequenzen, die sogenannten Formanten
Maximum in den Vielfachen der Grundfrequenz
Als Formanten werden die Resonanzfrequenzen der Vokaltrakt Transfer Funktion für eine bestimmte Konfiguration bezeichnet
Können stimmhaft oder stimmlos sein, können an deren Spektrum unterschieden werden
Die ersten beiden Formaten reichen aus um ein Vokal zu erkennen
Vokaldreieck
Trägt man 1. und 2. Formante auf x- und y-Achse auf kann man alle Vokale voneinander unterscheiden. Insgesamt bilden die Vokale dabei ein Dreieck, deshalb Vokaldreieck.
Frikative
Frikative sind eine Untergruppe der Phoneme, genau wie Vokale und Konsonanten. Frikative sind die sogenannten Reibelaute.

Frontend = Vorverarbeitung

Anti-Aliasing
AD Wandlung
Windowing
FFT
Energiespektrum bestimmen
Ziele: Geschwindigkeit, Genauigkeit

Speech Recognition

Gegeben: Akustische Daten A
Gesucht: Wordsequenz W
Lösungsansatz: basiert auf Bayes, P(W|A) maximal

Acoustic Model

HMM’s gehen nicht
Neuronale Netze (bzw. Hierachien von NNs) oder
Mixture Gaussians

Dictionaries

Word Dictionaries
Phonetic Dictionaries
Tree Structured Dictionaries (Faster Search)

Language Models

Grammatik-basiert
Vorteile
Lange Historie, größerer Context
Keine große Textdatenbank notwendig (Rapid Prototyping)
Nachteile
Viel Arbeit um Grammatik zu schreiben
Sehr strikt: Kann nur programmierte Regeln erkennen
N-Grams-basiert
Sagt anhand vorhergegangenen Wörtern nachfolgendes Wort voraus: 2-Grams, 3-Grams
P(w_i| w_{i-1}, w_{i-2}) (Trigram), P(w_i| w_{i-1}) (Bigram)
Vorteile
Trainierbar auf großen Textdatensätzen
Weiche Vorhersage basierend auf Wahrscheinlichkeiten
Kann direkt mit dem akustischen Modell kombiniert werden
Nachteile
Braucht eine große Textdatenbank für jede Domäne

Hidden Markov Model

Einsatzgebiet: Akustischen Einheiten der Sprache modellieren
Markov Annahme: Übergangswahrscheinlichkeit hängt nur vom aktuellen Zustand ab
Evaluation: Forward Algorithmus und Viterbi Algorithmus
Decoding: Viterbi Algorithmus
Training: Forward-Backward Algorithmus

Forward-Algorithmus

Trellis lösen, Aufgabenstellung: Welche Zeichenkette ist wahrscheinlicher?

Viterbi

Fragestellung: Welche Zustandsreihenfolge ist für eine Zeichenkette am wahrscheinlichsten?
Auch Forward-Algroithmus und Maximieren statt Aufsummieren

N-Grams

Nachteil: höhere Ordnung des N-Gramm-Modells -> Mehr Trainingsdaten (Erhöhung deshalb nicht immer möglich)
Viele Trainingsdaten notwendig um verlässliche Statistiken für alle möglichen Wortfolgen zu bestimmen
3-Gramm: P(w_i) = P(w_i|w_i-2,w_i-1)

Wortfehlerrate (WER)

#Ins + #Dels + #Subs
WER = _________________
N
* Nachteil von WER: Gewichtet alle Fehler gleich stark

Logik

Deduktion

Ein Algorithmus, der jede aus einer Wissensbasis folgerbare Aussage auch tatsächlich ableiten kann, heißt vollständig. Alle können abgeleitet werden.

Lassen sich mit einem Algorithmus nur Aussagen ableiten, die auch wirklich aus der Wissensbasis folgen, wird er als korrekt bezeichnet.

Resolution

Und-Oder-Graph: A v ~B v ~C -> B & C -> A (Körper-Kopf Regel)
Rückwärtsverkettung für Aussagefolgerung: Überprüfen ob gesuchte Aussage aus Fakten (Einzelliterale) folgt

Horn-Klauseln

Disjunktion von Literalen, von denen höchstens eins positiv ist
Typen
Fakt, Axiom (Keine negativen Literale)
Definition (genau ein positives Literal)
Integritätseinschränkung (kein positives Literal)
Nachteil: stellen nur eine Teilmenge der prädikatenlogischen Formeln dar (manche boolsche Funktionen kann man durch Hornklauseln nicht ausdrücken)

DPLL

Bahnplanung

Polygonzerlegung

Raum in Polygone zerlegen, indem von jeder Hindernisecke aus eine Trennlinie nach oben und unten bis zur nächsten Hinderniskante gezogen wird
Polygone sind entweder komplett frei oder komplett unpassierbar
Mittelpunkte jedes Freiraumpolygons sind Knoten im Suchgraph
A* Suche über Graph
Nachteil: Bei großen Freiräumen große Polygone, evtl. große Umwege

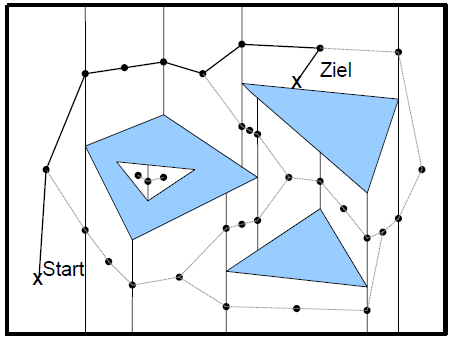
Sichtgraphen

Ecken sind Knoten des Graphen, Kante zu jedem Knoten der sichtbar ist
Ränder geometrischer Formen sind ebenfalls Kanten
Zur Wegsuche im Graph müssen die Kanten gewichtet werden -> Länge der Strecken
auch in R3 anwendbar, dann aber i.A. nicht mehr kürzeste Wege

Quadtrees

Aufteilung des Raumes in Quadrate (2D) bzw. Kuben (3D -> Octtrees) adaptiver Größe
Gesamter Raum als ein Quadrat, dieses wiederum in vier Unterquadrate aufteilen
Quadrat ist entweder komplett frei, komplett unpassierbar oder gemischt.
Falls gemischt, wieder unterteilen…

Voronoi-Diagramme

Ziel: Maximalen Abstand zu Hinternissen halten
Diagramm teilt Raum so in Flächen ein, dass jedes Hindernis in genau einer Fläche enthalten ist
Fläche enthält alle Punkte, für die dieses Hindernis das nächstgelegene ist
Grenzlinien erstellen:
punktförmige Hindernisse: eine Gerade
Punkt und Gerade: eine Parabel
Punkt und endlicher Strecke: eine Parabel im Streifen der Strecke, außerhalb Halbgerade
zwei Strecken:
Gerade im Schnitt der Streifen
Parabel bzgl. Endpunkt in einzelnem Streifen
Gerade bzgl. Endpunkten außerhalb der Streifen
ermittelter Weg garantiert maximale Freiheit von Hindernisse, aber evtl. großer Umweg

Potentialfeldmethode

Keine Überführung der Planungsaufgabe in Graphen
Stattdessen: Potentialfeld im Konfigurationsraum definieren, darin lokale Suche nach Gradientenabstieg
Ziel: globales Minimum, mit der Entfernung in alle Richtungen linear ansteigend
Hindernisse: hohes Potential, von Rändern aus mit der Entfernung kontinuierlich abnehmend

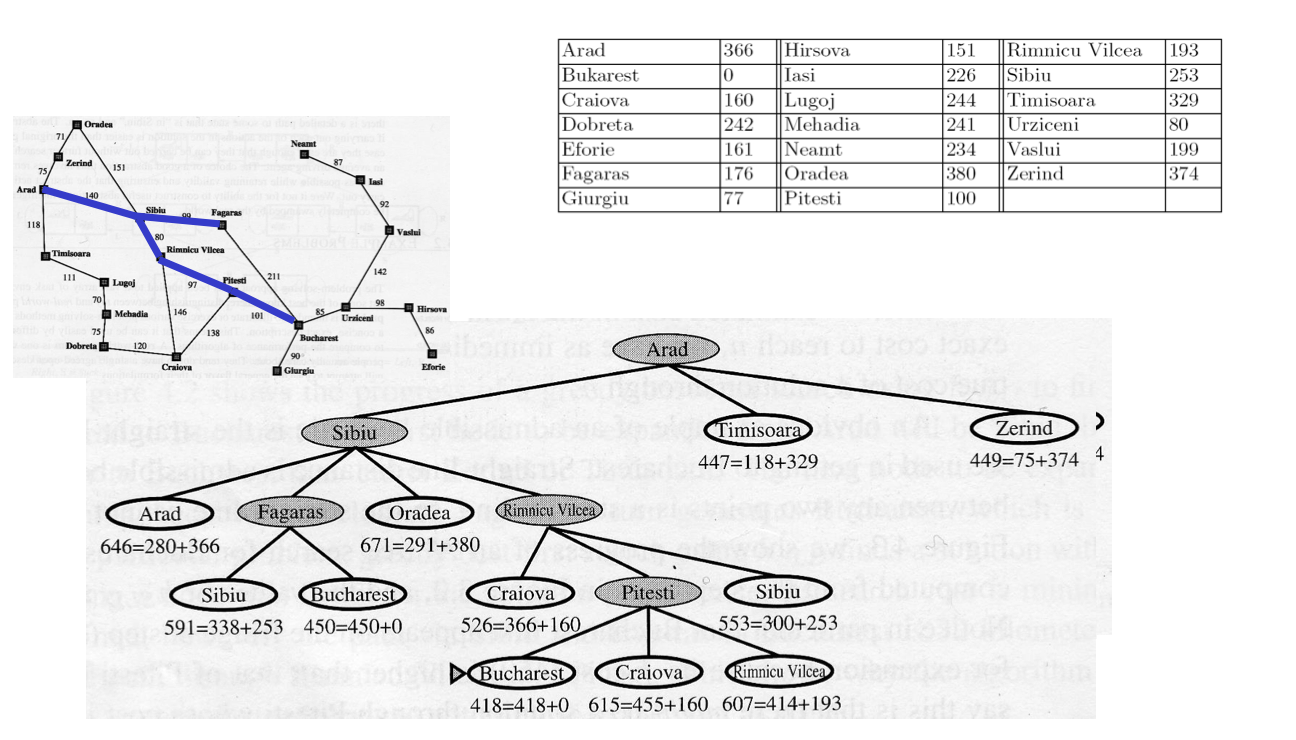
A*-Suche

Allgemeiner Algorithmus für die heuristikgestützte Suche in Graphen
Liefert kürzesten Weg zum Ziel
Effizienz abhängig von Güte der Heuristik
Expandiert den Knoten, für den die Summe (geschätzte Entfernung zum Ziel) + (bisher zurückgelegte Strecke vom Start) minimal ist
Es werden immer alle nicht-expandierten Knoten berücksichtigt (nicht nur der aktuelle Ast)

A-Suche

Robotik

(Nicht klausurrelevant!)